Addition binaire
Comme nous l'avions vu précédemment, le microprocesseur ne connaît que les chiffres 0 ou 1. Il ne peut donc faire des additions qu'avec ces deux chiffres. Ainsi, pour additionner 1 et 2, on pose l'addition suivante :
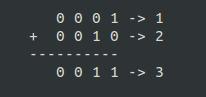
Comme pour les calculs dont on est habitué depuis la primaire, on effectue les calculs de droite à gauche. Ainsi, 1 + 0 = 1, donc le premier chiffre est 1. 0 + 1 = 1, le deuxième chiffre est également 1. Pour les deux derniers chiffres : 0 + 0 = 0, donc ceux-ci sont égals à 0. On obtient donc 0011, ce qui correspond au code binaire de 3.
Soustraction binaire
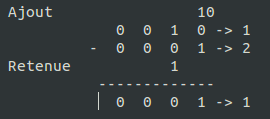
Le fonctionnement de la soustraction est le même qu'en primaire. Voici un exemple de soustraction binaire ( 2 – 1 ) :
Voici une vidéo explicative :
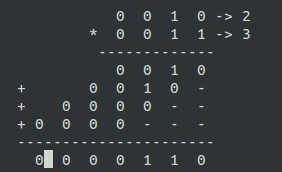
Multiplication binaire
La multiplication binaire suit, comme la plupart des formes de calcul binaire, des règles de bases apprises en primaire.
Division binaire
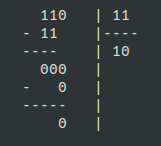
La division binaire suit les règles de la division euclidienne. Voici ci-dessous un exemple de division euclidienne (je divise ici 6 par 3) :