Modèle de boîte
Le code binaire n'est composé que de deux chiffres :
- 0 : Pas de courant
- 1 : Courant électrique
Pour les chiffres :
9 correspond à 1001 en langage binaire
Comment le 9 devient-il 1001 ?
Il faut considérer le code binaire comme une boîte, avec des
colonnes : (on commence avec une première boîte à droite
d’une valeur de 1 que l’on multiplie par deux, pour la valeur de
la boîte suivante, et ainsi de suite…) Sur les ordinateur 64bit, il
y a ainsi 64 boîte, la 64ème boîte correspond à
![]() et des poussières...
et des poussières...
|
|
|
|
|
|
|
|||
|
|
|||
|
|
|||
|
|
|
||
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
8 |
4 |
2 |
1 |
9 correspond à neuf boules, et l'on commence toujours par remplir les plus grandes boîtes :
|
9 |
2 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Pour les lettres : Chaque lettre correspond à un chiffre, par exemple 74 pour le J : 0100 1010
La logique du code binaire
La logique du code binaire :
Le code binaire suit une logique relativement simple : en tant qu'humain, nous comptons de la manière suivante, avec dix chiffres :
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...
L'ordinateur, lui va compter de la manière suivante (avec seulement deux chiffres) :
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001
En résumé :
|
Chiffre humain |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Correspondance en binaire |
0 |
1 |
10 |
11 |
100 |
101 |
110 |
111 |
1000 |
1001 |
|
Code binaire |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
1000 |
1001 |
Ensemble du code binaire
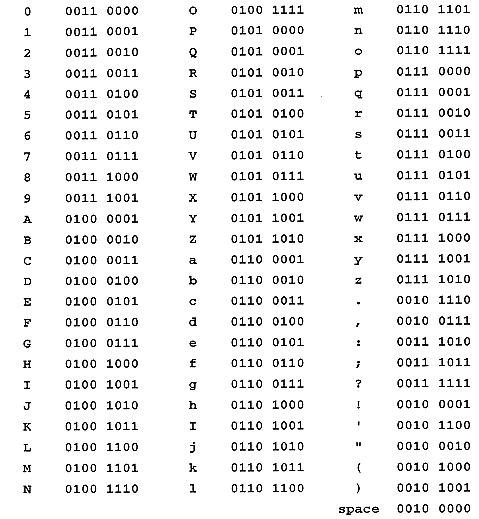
Image disponible à l'adresse http://www.cs.ndsu.nodak.edu/~adenton/ExpandingHorizons/EH2005/ascii-binary-chart.gif